Gas laws:
Posted: 5 March 2021
“Observe what happens when sunbeams are admitted into a building and shed light on its shadowy places. You will see a multitude of tiny particles mingling in a multitude of ways… their dancing is an actual indication of underlying movements of matter that are hidden from our sight… It originates with the atoms which move of themselves [i.e., spontaneously]. Then those small compound bodies that are least removed from the impetus of the atoms are set in motion by the impact of their invisible blows and in turn cannon against slightly larger bodies. So the movement mounts up from the atoms and gradually emerges to the level of our senses so that those bodies are in motion that we see in sunbeams, moved by blows that remain invisible”
Lucretius
Lucretus was one of, if not the first, person to record the effects that we now refer to as “Brownian motion” – the random motion of particles suspended in a medium (a liquid or a gas) as a result of their random bombardment by the smaller (usually invisible) particles that make up the medium. The origional greek term “pedesis” meaning “leaping” describes the motion more aptly.
This leaping motion is the first piece of evidence we use to justify the model of all gaseous behaviour. Daniel Bernoulli, in 1738, was the first to really use this model to understand air pressure in terms of molecules— he visualized them shooting around very rapidly in a closed container, supporting a weight by constantly bouncing off the underside of the piston. He came extremely close to our modern understanding using the logic of the model – “Given more room, they would rush in to fill the new space, just as a gas is observed to do.” It is a tragic, and oft-repeated fact – that the work went no further as he was unable to convince anyone to belie him.
These days we’re very familliar with the idea of solids, liquids, and gasses being modelled in this way:

Historically however, it takes the industrial revolution, and the interest in more efficient steam engines, to really drive our understanding of gasses…

Boyle is largely regarded today as the first modern chemist, and therefore one of the founders of modern chemistry, and one of the pioneers of modern experimental scientific method. On reading in 1657 of the invention of an air pump by Otto von Guericke he set himself to devise improvements in its construction, along with his assistant, Robert Hooke (yes that Hooke). The result of their experiments were published in the manuscript you see above in which is described Boyle’s most famous legacy – Boyle’s Law:
There is an inversely proportional relationship between the absolute pressure and volume of a gas, if the temperature is kept constant within a closed system.
In other words:
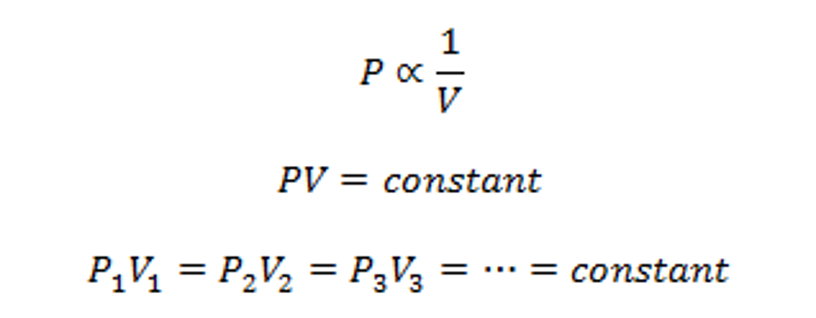
Charles’ Law:
At around the same time, others in the world of science were experimenting with pressures and volumes.
in his unpublished work Jaques Charles was slightly ahead of the scientist John Dalton who demonstrated by experiment that all the gases and vapours that he studied expanded by the same amount between two fixed points of temperature. The French natural philosopher Joseph Louis Gay-Lussac confirmed the discovery in a presentation to the French National Institute on 31 Jan 1802, although he credited the discovery to unpublished work from the 1780s by Jacques Charles. (note however that the basic principles had already been described by Guillaume Amontons and Francis Hauksbee a century earlier – such is the nature of scientific development).
In short this relationship tells us that at any given temperature the density of a gas is related to it’s temperature:

In mathematical terms:
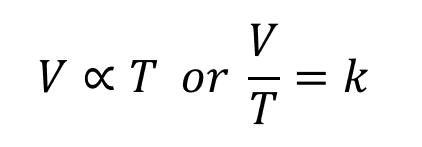
Amonton’s law, or often, the Gay-Lussac law
A few lines ago we mentioned Amonton and the demonstrations by Joseph Louis Gay-Lussac to the French National Institute. Whilst Gay-Lussac credited others for some work, he either omitted, or was unaware of the work by Amonton to show the relationship between the pressure and temperature of a fixed mass of gas kept at a constant volume
The pressure of a gas of fixed mass and fixed volume is directly proportional to the gas’s absolute temperature.
If a gas’s temperature increases, then so does its pressure if the mass and volume of the gas are held constant. In the picture below the coke can has been allowed to sit in the sunshine until the pressure inside rose sufficiently to deform the material of the container. beware if trying to illustrate this as the container is likely to rupture explosively!

The law has a particularly simple mathematical form if the temperature is measured on an absolute scale, such as in kelvins. The law can then be expressed mathematically as P = kT
Putting these three together and we are almost at a complete model of gasses:
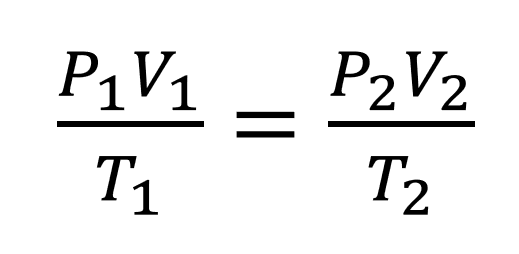
Our final piece of the jigsaw comes from Avogadro:

Putting it all together we finally arrive at our mathematical model of an ideal gas:
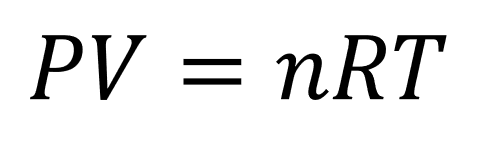
Pressure, p
Pressure is measured in pascals, Pa – sometimes expressed as newtons per square metre, N m-2. These mean exactly the same thing.
Be careful if you are given pressures in kPa (kilopascals). For example, 150 kPa is 150000 Pa. You must make that conversion before you use the ideal gas equation.
Should you want to convert from other pressure measurements:
1 atmosphere = 101325 Pa
1 bar = 100 kPa = 100000 Pa
Volume, V
This is the most likely place for you to go wrong when you use this equation. That’s because the SI unit of volume is the cubic metre, m3 – not cm3 or dm3.
1 m3 = 1000 dm3 = 1 000 000 cm3
So if you are inserting values of volume into the equation, you first have to convert them into cubic metres.
You would have to divide a volume in dm3 by 1000, or in cm3 by a million.
Similarly, if you are working out a volume using the equation, remember to covert the answer in cubic metres into dm3 or cm3 if you need to – this time by multiplying by a 1000 or a million.
If you get this wrong, you are going to end up with a silly answer, out by a factor of a thousand or a million. So it is usually fairly obvious if you have done something wrong, and you can check back again.
Number of moles, n
This is easy, of course – it is just a number. You already know that you work it out by dividing the mass in grams by the mass of one mole in grams.
You will most often use the ideal gas equation by first making the substitution to give:
I don’t recommend that you remember the ideal gas equation in this form, but you must be confident that you can convert it into this form.
The gas constant, R
A value for R will be given you if you need it, or you can look it up in a data source. The SI value for R is 8.31441 J K-1 mol-1.
Note: You may come across other values for this with different units. A commonly used one in the past was 82.053 cm3 atm K-1 mol-1. The units tell you that the volume would be in cubic centimetres and the pressure in atmospheres. Unfortunately the units in the SI version aren’t so obviously helpful.
The temperature, T
The temperature has to be in kelvin. Don’t forget to add 273 if you are given a temperature in degrees Celsius.

